DataSurg

19/04/201325/02/2015

Tweets of Surgical Colleges – what does it say about them?

What do the UK and Ireland Surgical Royal Colleges tweet about and how do they compare to the American College of Surgeons?

Twitter allow retrieval of the last 3200 tweets of a given user. Here are all tweets ever sent by the Royal Colleges a few days ago. The American College has tweeted over 6000 times, so only the latest 3200 are included. The Glasgow College is just getting going.

There is a bit of processing first. Charts are generated after removal of “stop words” – all the little words that go in between. Words then have common endings removed (e.g. -ing; stemming) and the most common ending for the group replaced (stem completion).

So what can be said? I was interested in whether Colleges tweet about training. I was pleased to see that the UK colleges do – a fair amount. Terms that are associated with training were less apparent in tweets from the RCSI and ACS.

Frequency of words in tweets from five surgical colleges

The figures below show clustering of terms within tweets, with term frequency increasing from left to right. There are some nice themes that emerge. In the RCSEng tweets there are themes relating to “training”, “events”, “working time”, and “the NHS”. Similar subjects are apparent in RCSEd tweets, with prominence of their medical students surgical skill competition and issues specifically relating to the NHS in Scotland. As the RCPSG have only started tweeting, associations are greatly influenced by individual tweets. The RCSI’s ~~“Transition Year Mini Med School Programme”~~ “MiniMed School Open Lecture Series” (updated 22/04/13) can be seen together with conference promotion. The ACS appear to use Twitter to communicate issues relating to patient health improvement programmes more prominently than other Colleges.

Term association in surgical college tweets (cluster dendrogram)

Network plots illustrate the strength of association of terms (weight of edges) and frequency of terms (font size of vertices). Do the terms in these plots represent the core values of these organisations?

12/04/201312/04/2013

Publication of paediatric cardiac surgery results

The National Institute for Cardiovascular Outcomes Research (NICOR) has published the results of its investigation into mortality after paediatric heart surgery in England 2009-12.

The short report has two main findings – the quality of data collection at Leeds General Infirmary (LGI) was woeful, and differences in mortality between all hospitals are likely to be explained by natural variation.

The ability of an institution to collect and audit its own results can be viewed as a measure of organisational health. As can be seen in the table, the performance of LGI in this respect was terrible, and much worse than other units. A cause for concern in itself.

On the more controversial point of whether the mortality rate in LGI was worse than other centres, no convincing proof of this has been found.

The funnel plot below shows the number of expected deaths along the bottom. Centres performing greater numbers of procedures have a greater number of expected deaths, just by common sense.

These numbers have been corrected for the difference in the types of patients and surgery performed in hospitals – the specific procedure performed, patient age, weight, diagnosis, and previous medical conditions. All these factors impact on the risk of death following surgery.

Any hospital above the black horizontal line has a greater number of deaths than predicted and any hospital below has fewer.

By “the law of averages”, it would be expected that there was a roughly equal spread of hospitals above and below the line.

As can be seen, Alder Hey, Guys, and LGI are all close to triggering an “alert”.

The report rightly states that these units “may deserve additional scrutiny and monitoring of current performance”.

The 3-year risk adjusted mortality rate in LGI is 1.47 times the national average – lower than the “twice the national average” first reported.

The unambiguous message? Data collection and real-time analysis is core business in healthcare. Government and the NHS still do not have a grip of this. There are many more stories of significant differences between hospitals, hidden in poor quality data that no one is looking at.

06/04/201307/04/2013

Mortality after paediatric heart surgery using public domain data

This post comes with some big health warnings.

The recent events in Leeds highlight the difficulties faced in judging the results of surgery by individual hospital. A clear requirement is timely access to data in a form easily digestible by the public.

Here I’ve scraped the publically available data from the central cardiac audit database (CCAD). All the data are available at the links provided and are as presented this afternoon (06/04/2013). Please read the caveats carefully.

Hospital-specific 30-day mortality data are available for certain paediatric heart surgery procedures for 2009-2012. These data are not complete for 2011-12 and there may be missing data for earlier years. There may be important data for procedures not included here that should be accounted for. There is no case-mix adjustment.

All data are included in spreadsheets below as well as the code to run the analysis yourself, to ensure no mistakes have been made. Hopefully these data will be quickly superseded with a quality-assured update.

Mortality by centre

The funnel plot below has been generated by taking all surgical procedures performed from pages such as this and expressing all deaths within 30 days as a proportion of the total procedures performed by hospital.

The red horizontal line is the mean mortality rate for these procedures – 2.3%. The green, blue and red curved lines are decreasingly stringent control limits within which unit results may vary by chance.

Mortality by procedure

The mortality associated with different procedures can be explored with this google motion chart. Note when a procedure is uncommon (to the left of the chart) the great variation seen year to year. These bouncing balls trace out the limits of a funnel plot. They highlight why year to year differences in mortality rates for rare procedures must be interpreted with caution.

[cf]googleVis[/cf]

Data

ccad_public_data_april_2013.xls

ccad_public_data_april_2013_centre

ccad_public_data_april_2013_aggregate

ccad_public_data_april_2013_lookup

Script

####################################
# CCAD public domain data analysis #
# 6 April 2013                     #
# Ewen Harrison                    #
# www.datasurg.net                 #
#################################### 

# Read data
data<-read.table("ccad_public_data_april_2013_centre.csv", sep=",", header=TRUE)

# Correct variable-type
data$centre_code<-factor(data$centre_code)

# Read centre names table
centre<-read.table("ccad_public_data_april_2013_lookup.csv", sep=",", header=TRUE)

# Combine
data<-merge(data, centre, by="centre_code")

# Subset by only procedures termed "Surgery" and remove procedures with no data. 
surg<-subset(data, type=="Surgery" & !is.na(data$centre_code))

# Display data
surg
str(surg)

# install.packages("plyr") # remove "#" first time to install
library(plyr)

# Aggregate data by centre
agg.surg<-ddply(surg, .(centre_code), summarise, observed_mr=sum(death_30d)/sum(count), 
  sum_death=sum(death_30d), count=sum(count))

# Overall mortality rate for procedures lists in all centres
mean.mort<-sum(surg$death_30d)/sum(surg$count)
mean.mort #2.3%

# Generate binomial confidence limits

# install.packages("binom") # remove "#" first time to install
library(binom)
binom_n<-seq(90, 1100, length.out=40)
ci.90<-binom.confint(mean.mort*binom_n, binom_n, conf.level = 0.90, methods = "agresti-coull")
ci.95<-binom.confint(mean.mort*binom_n, binom_n, conf.level = 0.95, methods = "agresti-coull")
ci.99<-binom.confint(mean.mort*binom_n, binom_n, conf.level = 0.997, methods = "agresti-coull")

# Plot chart
# install.packages("ggplot2") # remove "#" first time to install
library(ggplot2)
ggplot()+
	geom_point(data=agg.surg, aes(count,observed_mr))+
	geom_line(aes(ci.90$n, ci.90$lower, colour = "90% CI"))+ #hack to get legend
	geom_line(aes(ci.90$n, ci.90$upper), colour = "green")+
	geom_line(aes(ci.95$n, ci.95$lower, colour = "95% CI"))+ 
	geom_line(aes(ci.95$n, ci.95$upper), colour = "blue")+
	geom_line(aes(ci.99$n, ci.99$lower, colour = "99.7% CI"))+ 
	geom_line(aes(ci.99$n, ci.99$upper), colour = "red")+
	geom_text(data=agg.surg, aes(count,observed_mr,label=centre_code), size=3,vjust=-1)+
	geom_line(aes(x=90:1100, y=mean.mort), colour="red")+
	ggtitle("Observed mortality rate following paediatric heart surgery\nby centre using CCAD public domain data 2009-2012 (incomplete)")+
	scale_x_continuous(name="Number cases performed per centre 2009-2012", limits=c(90,1100))+
	scale_y_continuous(name="Observed mortality rate")+
	scale_colour_manual("",
		breaks=c("90% CI", "95% CI", "99.7% CI"),
		values=c("green", "blue", "red"))+
	theme_bw()+
	theme(legend.position=c(.9, .9))

# Google motion chart
# Load national aggregate data by procedure
agg_data<-read.table("ccad_public_data_april_2013_aggregate.csv", sep=",", header=TRUE)

# check
str(agg_data)

# install.packages("googleVis") # remove "#" first time to install
library(googleVis)
Motion=gvisMotionChart(agg_data, idvar="procedure", timevar="year",
	options=list(height=500, width=600,
		state='{"showTrails":true,"yZoomedDataMax":1,"iconType":"BUBBLE","orderedByY":false,"playDuration":9705.555555555555,"xZoomedIn":false,"yLambda":1,"xAxisOption":"3","nonSelectedAlpha":0.4,"xZoomedDataMin":0,"iconKeySettings":[],"yAxisOption":"5","orderedByX":false,"yZoomedIn":false,"xLambda":1,"colorOption":"2","dimensions":{"iconDimensions":["dim0"]},"duration":{"timeUnit":"Y","multiplier":1},"xZoomedDataMax":833,"uniColorForNonSelected":false,"sizeOption":"3","time":"2000","yZoomedDataMin":0.33};'),
		chartid="Survival_by_procedure_following_congenital_cardiac_surgery_in_UK_2000_2010")
plot(Motion)

03/04/2013

Two simple tests for summary data

Here’s two handy scripts for hypothesis testing of summary data. I seem to use these a lot when checking work:

Chi-squared test of association for categorical data.
Student’s t-test for difference in means of normally distributed data.

The actual equations are straightforward, but get involved when group sizes and variance are not equal. Why do I use these a lot?!

I wrote about a study from Hungary in which the variability in the results seemed much lower than expected. We wondered whether the authors had made a mistake in saying they were showing the standard deviation (SD), when in fact they had presented the standard error of the mean (SEM).

This is a bit of table 1 from the paper. It shows the differences in baseline characteristics between the treated group (IPC) and the active control group (IP). In it, they report no difference between the groups for these characteristics, p>0.05.

But taking “age” as an example and using the simple script for a Student’s t-test with these figures, the answer we get is different. Mean (SD) for group A vs. group B: 56.5 (2.3) vs. 54.8 (1.8), t=4.12, df=98, p=<0.001.

There are lots of similar examples in the paper.

Using standard error of the mean rather than standard deviation gives a non-significant difference as expected.

$latex SEM=SD/\sqrt{n}.$

See here for how to get started with R.

####################
# Chi-sq test from #
# two by two table #
####################

#           Factor 1
# Factor 2  a   |   b
#           c   |   d

a<-32
b<-6
c<-43
d<-9

m<-rbind(c(a,b), c(c,d))
m
chisq.test(m, correct = FALSE)
# Details here
help(chisq.test)

############################
# T-test from summary data #
############################

# install.packages("BSDA") # remove first "#" to install first time only
library(BSDA)
x1<-56.5     # group 1 mean
x1_sd<-2.3   # group 1 standard deviation
n1<-50       # group 1 n
x2<-54.8     # group 2 mean
x2_sd<-1.8   # group 2 standard deviation
n2<-50       # group 2 n

tsum.test(x1, x1_sd, n1, x2, x2_sd, n2, var.equal = TRUE)
# Details here
help(tsum.test)

03/04/201303/04/2013

Statistical errors in published medical studies

I do a fair amount of peer-review for journals. My totally subjective impression – which I can’t back up with figures – is that fundamental errors in data analysis occur on a fairly frequent basis. Opaque descriptions of methods and no access to raw data often makes errors difficult to detect.

We’re performing a meta-analysis at the moment. This is a study in which two or more clinical trials of the same treatment are combined. This can be useful when there is uncertainty about the effectiveness of a treatment.

Relevent trials are rigorously searched for and the quality assessed. The results of good quality trials are then combined, usually with more weight being given to the more reliable trials. This weight reflects the number of patients in the trial and, for some measures, the variability in the results. This variation is important – trials with low variability are greatly influential in the final results of the meta-analysis.

What are we doing the meta-analysis on? We often operate to remove a piece of liver due to cancer. Sometimes we have to clamp the blood supply to the liver to prevent bleeding. An obvious consequence to this is damage to the liver tissue.

Multiple local liver resections. Patient provided consent for image publication.

It may be possible to protect the liver (and any organ) from these damaging effects by temporarily clamping the blood supply for a short time, then releasing the clamp and allowing blood to flow back in. The clamp is then replaced and the liver resection performed. This is called “ischemic preconditioning” and may work by stimulating liver cells to protect themselves. “Batten down the hatches boys, there’s a storm coming!”

Results of this technique are controversial – when used in patients some studies show it works, some show no benefit. So should we be using it in our day-to-day practice?

We searched for studies examining ischemic preconditioning and found quite a few.

One in particularly performed by surgeons in Hungary seemed to show that the technique worked very well (1).The variability in this study was low as well, so it seemed reliable. Actually the variability was very low – lower than all the other trials we found.

Variation in biochemical outcome measures in studies of ischemic preconditioning.

The graph shows 3 of the measures used to determine success of the preconditioning. The first two are enzymes released from damaged liver cells and the third, bilirubin, is processed by the liver. All the studies show some lowering of these measures signifying potential improvement with the treatment. But most trials show a lot of variation between different patients (the vertical lines).

Except a Hungarian study, which shows almost no variation.

Even compared with a study in which these tests were repeated between healthy individuals in the US (9), the variation was low. That seemed strange. Surely the day-to-day variation in your or my liver tests should be lower than those of a group of patients undergoing surgery?

It looks like a mistake.

It may be that the authors wrote that they used one measure of variation when they actually used another (standard error of the mean vs. standard deviation). This could be a simple mistake, the details are here.

But we don’t know. We wrote three times, but they didn’t get back to us. We asked the journal and they are looking into it.

1 Hahn O, Blázovics A, Váli L, et al. The effect of ischemic preconditioning on redox status during liver resections-randomized controlled trial. Journal of Surgical Oncology 2011;104:647–53.
2 Clavien P-A, Selzner M, Rüdiger HA, et al. A Prospective Randomized Study in 100 Consecutive Patients Undergoing Major Liver Resection With Versus Without Ischemic Preconditioning. Annals of Surgery 2003;238:843–52.
3 Li S-Q, Liang L-J, Huang J-F, et al. Ischemic preconditioning protects liver from hepatectomy under hepatic inflow occlusion for hepatocellular carcinoma patients with cirrhosis. World J Gastroenterol 2004;10:2580–4.
4 Choukèr A, Martignoni A, Schauer R, et al. Beneficial effects of ischemic preconditioning in patients undergoing hepatectomy: the role of neutrophils. Arch Surg 2005;140:129–36.
5 Petrowsky H, McCormack L, Trujillo M, et al. A Prospective, Randomized, Controlled Trial Comparing Intermittent Portal Triad Clamping Versus Ischemic Preconditioning With Continuous Clamping for Major Liver Resection. Annals of Surgery 2006;244:921–30.
6 Heizmann O, Loehe F, Volk A, et al. Ischemic preconditioning improves postoperative outcome after liver resections: a randomized controlled study. European journal of medical research 2008;13:79.
7 Arkadopoulos N, Kostopanagiotou G, Theodoraki K, et al. Ischemic Preconditioning Confers Antiapoptotic Protection During Major Hepatectomies Performed Under Combined Inflow and Outflow Exclusion of the Liver. A Randomized Clinical Trial. World J Surg 2009;33:1909–15.
8 Scatton O, Zalinski S, Jegou D, et al. Randomized clinical trial of ischaemic preconditioning in major liver resection with intermittent Pringle manoeuvre. Br J Surg 2011;98:1236–43.
9 Lazo M, Selvin E, Clark JM. Brief communication: clinical implications of short-term variability in liver function test results. Ann Intern Med 2008;148:348–52.

31/03/201301/04/2013

Leeds paediatric heart surgery: managing outliers

Childrens’ heart surgery in Leeds has been suspended. Concerns about an excess in mortality have been raised and denied and I have written about seemingly large variations in mortality (“twice the national average”) being explained by chance.

In June 1998, the then Secretary of State for Health announced the establishment of an inquiry into the management of the care of children receiving complex cardiac surgery at Bristol Royal Infirmary between 1984 and 1995. The inquiry identified failures that contributed to the death children undergoing heart surgery and the 529-page report was a blueprint for wider reform of the NHS.

Funnel plots are useful for comparing the results of surgery between hospitals. The funnel plots below are from here and are for open cardiac surgery in children under one year in the UK 1991-1995. The Cardiac Surgery Registry (CSR) and Hospital episode statistics (HES) data were used to compare institutions. The horizontal dotted line is the national average and curved dotted line the limit of variation which might be expected by chance (95% confidence interval). The “O” is Bristol Royal Infirmary and “*” the eleven other UK centres. Bristol, as became apparent, was a clear outlier.

Funnel plots for open congenital heart surgery in chilldren under 1 year in UK 1991-1995

How should we deal with outliers?

The question is pertinent given the recent suspension of Leeds Royal Infirmary from performing children’s cardiac surgery. The UK Department of Health has produced guidelines in 2011 on the recommended process should a unit hit the dotted line, summarised below.

Stage 1 | 10 days

Hospitals with a performance indicator ‘alert’ or ‘alarm’ require scrutiny of the data handling and analyses performed to determine whether there is:

‘No case to answer’

potential outlier status not confirmed;
data and results revised in clinical audit records;
details formally recorded.

‘Case to answer’

potential outlier status;
proceed to stage 2.

Stage 2 | 5 days

The Lead Clinician in the hospital is informed about the potential outlier status and requested to identify any data errors or justifiable explanations. All relevant data and analyses should be made available to the Lead Clinician.

A copy of the request should also be sent to the Clinical Governance Lead of the hospital.

Stage 3 | 25 days

Lead Clinician to provide written response to national clinical audit team.

Stage 4 | 30 days

Review of Lead Clinician’s response to determine:
‘No case to answer’

It is confirmed that the data originally supplied by the provider contained inaccuracies. Reanalysis of accurate data no longer indicate outlier status;
Data and results should be revised in clinical audit records. Details of the hospital’s response and the review result recorded;
Lead Clinician notified in writing.

‘Case to answer’

It is confirmed that although the data originally supplied by the provider were inaccurate, analysis still indicates outlier status; or
It is confirmed that the originally supplied data were accurate, thus confirming the initial designation of outlier status;
proceed to stage 5.

Stage 5 | 5 days

Contact Lead Clinician by telephone, prior to written confirmation of potential outlier status; copied to clinical governance lead, medical director and chief executive. All relevant data and statistical analyses, including previous response from the lead clinician, made available to the medical director and chief executive.

Chief executive advised to inform relevant bodies about the concerns: primary care trusts, Strategic Health Authority, professional society/association, and Care Quality Commission. Informed that the audit body will proceed to publishing information of comparative performance that will identify providers.

Stage 6 | 10 days

Chief executive acknowledgement of receipt of the letter.

Stage 7

Public disclosure of comparative information that identifies providers (eg annual report of NCA).

The Situation in Leeds

It appears that in Leeds the process is at stage 2 – the local doctors have just been informed. The guidance suggests the identity of the statistical outliers should be anonymous at this stage. It may be that concerns were so great that special circumstances dictated the dramatic public announcement. We should find out in the next few weeks.

31/03/201301/04/2013

R function to retrieve pubmed citations from pmid number

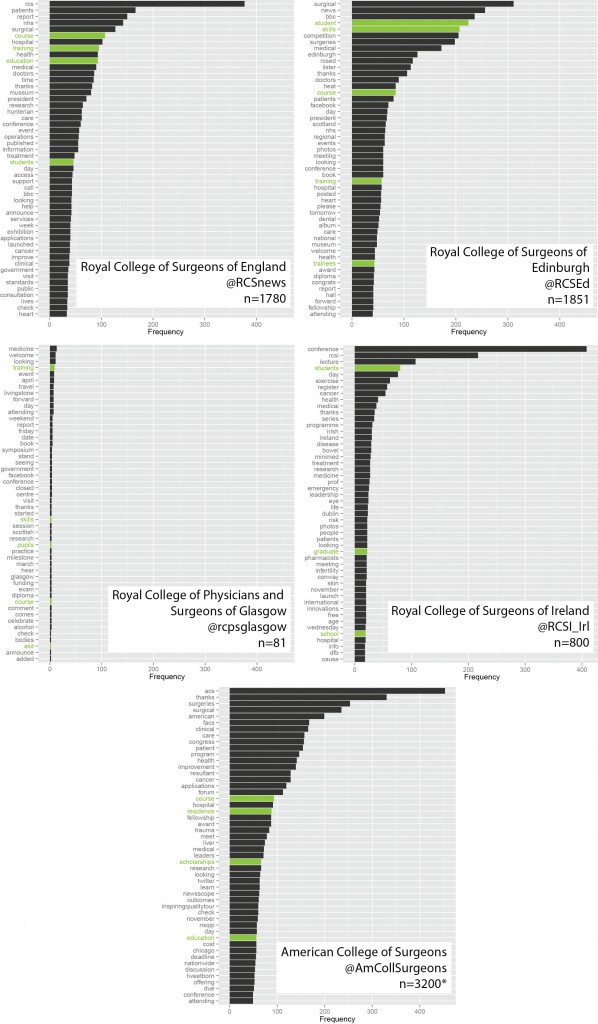
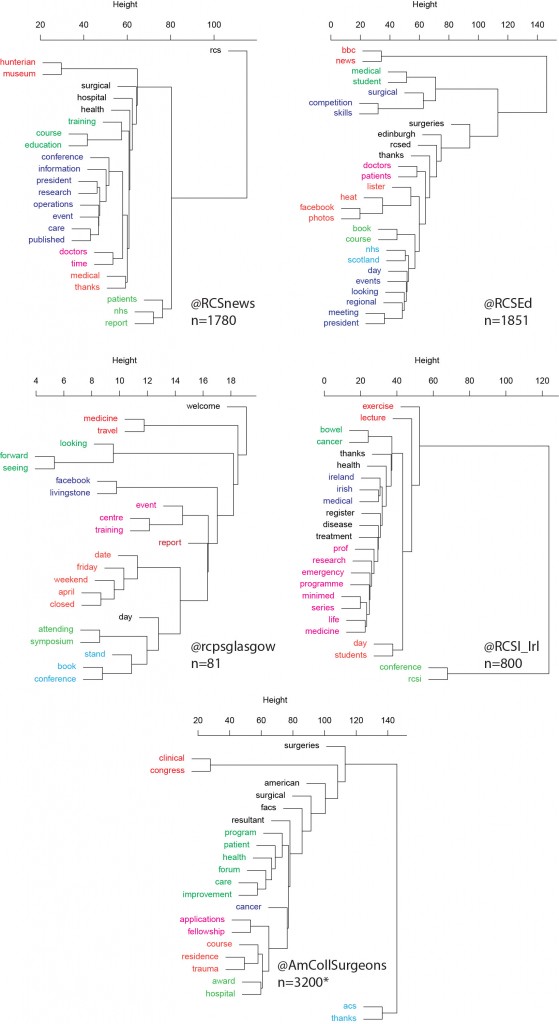
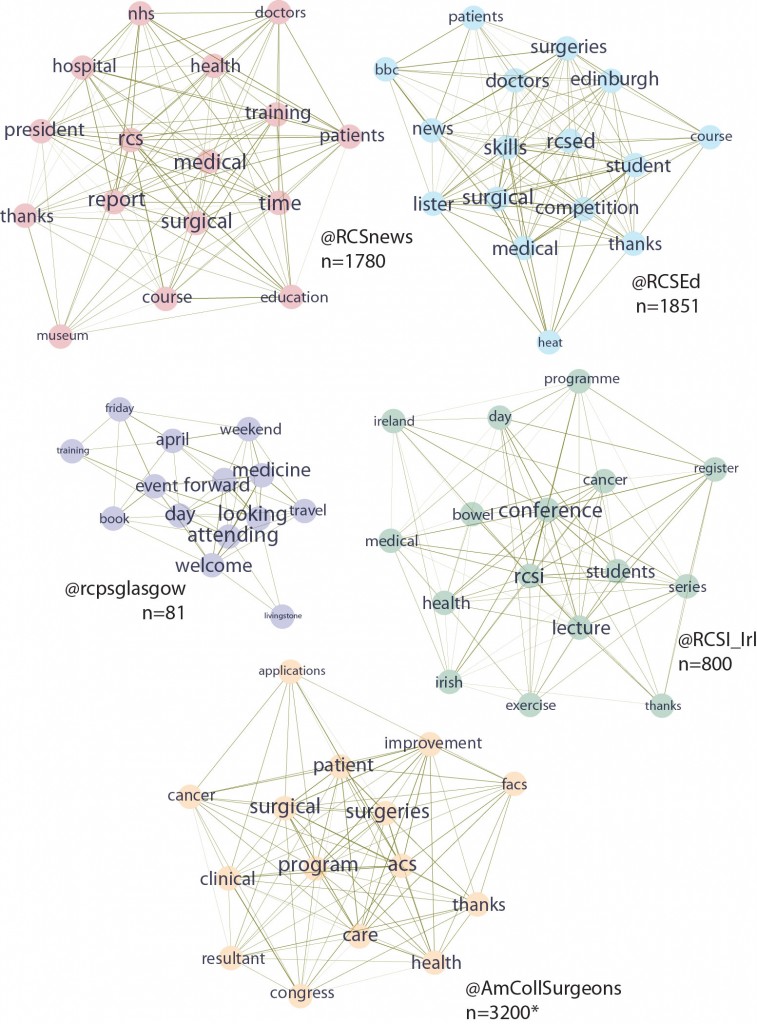
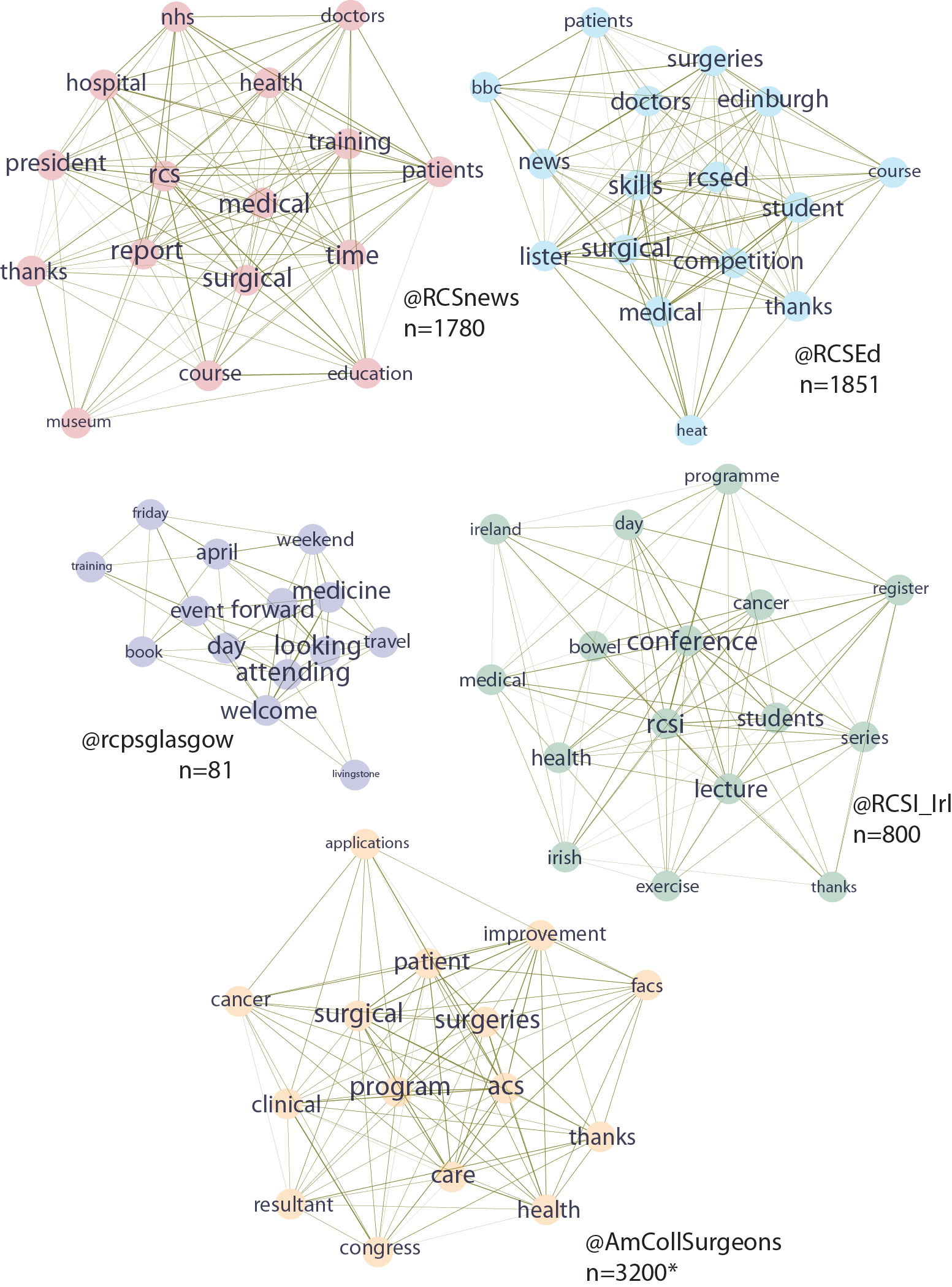
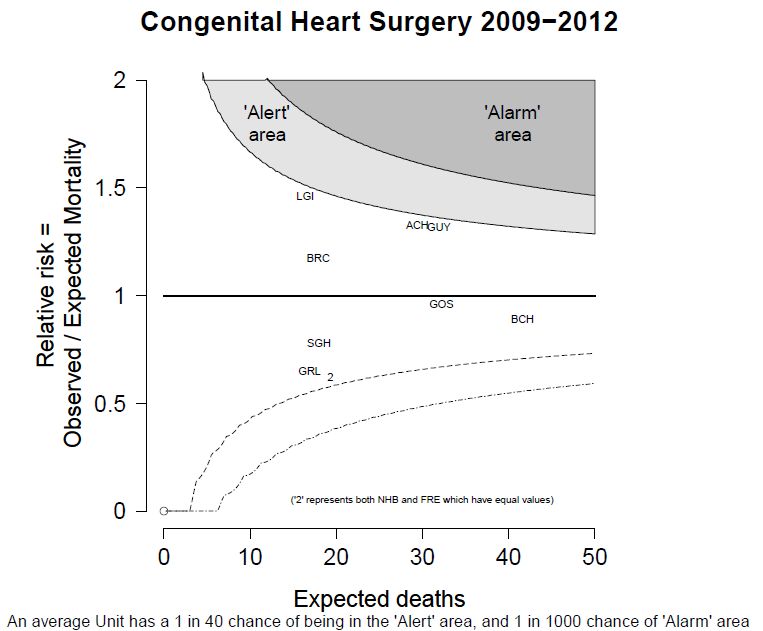
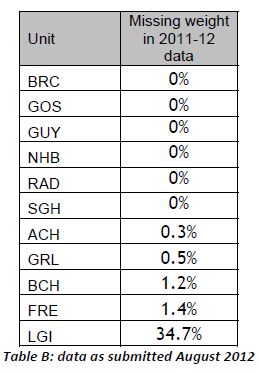
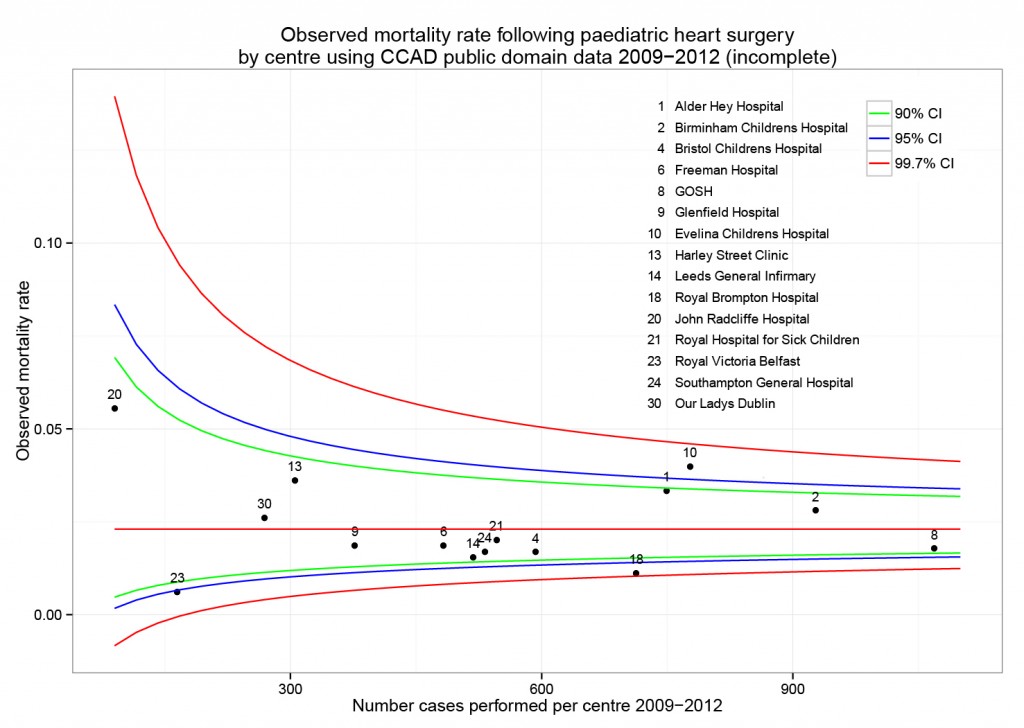
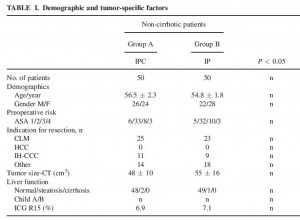
This is useful number if you have hundreds of PMIDs and need specific fields from the pubmed/medline citation.

#################################
# Retrieve pubmed citation data #
# Ewen Harrison                 #
# March 2013                    #
# www.datasurg.net              #
#################################

# Sample data
pmid<-c(8339401,8485120,8427851,3418853,3195585,2643302,7947591,8274474,8243847)
#-----------------------------------------------------------------------------------------------------------------------------------
# Batch list of PMIDs into groups of 200
fn_batch<-function(pmid=pmid,n=200){
	require(plyr)	
	b<-list()
	max=ceiling(length(pmid)/n)
	for (i in 1:max){
		b[[i]]<-pmid[(1+((i-1)*n)):(n*i)]
	}
	b[[max]]<-b[[max]][!is.na(b[[max]])]	# drop missing values in the final block
	c<-llply(b, function(a){			# convert from list to comma separted list
		paste(a, collapse=",")
	})
	return(c)
}
#-----------------------------------------------------------------------------------------------------------------------------------
# Run
pmid_batch<-fn_batch(pmid)
#-----------------------------------------------------------------------------------------------------------------------------------
# Function to fetch, parse and extract medline citation data. Use wrapper below.
get_pubmed<-function(f){
	require(RCurl)
	require(XML)
	require(plyr)
		# Post PMID (UID) numbers
	url<-paste("http://eutils.ncbi.nlm.nih.gov/entrez/eutils/efetch.fcgi?db=pubmed&id=", f, "&retmode=XML", sep="")
		# Medline fetch
	g<-llply(url, .progress = progress_tk(label="Fetching and parse Pubmed records ..."), function(x){
		xmlTreeParse(x, useInternalNodes=TRUE)
		})
		# Using given format and xml tree structure, paste here the specific fields you wish to extract
	k<-ldply(g, .progress = progress_tk(label="Creating dataframe ..."), function(x){
		a<-getNodeSet(x, "/PubmedArticleSet/*/MedlineCitation")
		pmid_l<-sapply (a, function(a) xpathSApply(a, "./PMID", xmlValue))
		pmid<-lapply(pmid_l, function(x) ifelse(class(x)=="list" | class(x)=="NULL", NA, x))
		nct_id_l<-sapply (a, function(a) xpathSApply(a, "./Article/DataBankList/DataBank/AccessionNumberList/AccessionNumber", xmlValue))
		nct_id<-lapply(nct_id_l, function(x) ifelse(class(x)=="list" | class(x)=="NULL", NA, x))
		year_l<-sapply (a, function(a) xpathSApply(a, "./Article/Journal/JournalIssue/PubDate/Year", xmlValue))
		year<-lapply(year_l, function(x) ifelse(class(x)=="list" | class(x)=="NULL", NA, x))
		month_l<-sapply (a, function(a) xpathSApply(a, "./Article/Journal/JournalIssue/PubDate/Month", xmlValue))
		month<-lapply(month_l, function(x) ifelse(class(x)=="list" | class(x)=="NULL", NA, x))
		day_l<-sapply (a, function(a) xpathSApply(a, "./Article/Journal/JournalIssue/PubDate/Day", xmlValue))
		day<-lapply(day_l, function(x) ifelse(class(x)=="list" | class(x)=="NULL", NA, x))
		year1_l<-sapply (a, function(a) xpathSApply(a, "./Article/ArticleDate/Year", xmlValue))
		year1<-lapply(year1_l, function(x) ifelse(class(x)=="list" | class(x)=="NULL", NA, x))
		month1_l<-sapply (a, function(a) xpathSApply(a, "./Article/ArticleDate/Month", xmlValue))
		month1<-lapply(month1_l, function(x) ifelse(class(x)=="list" | class(x)=="NULL", NA, x))
		day1_l<-sapply (a, function(a) xpathSApply(a, "./Article/ArticleDate/Day", xmlValue))
		day1<-lapply(day1_l, function(x) ifelse(class(x)=="list" | class(x)=="NULL", NA, x))
		medlinedate_l<-sapply (a, function(a) xpathSApply(a, "./Article/Journal/JournalIssue/PubDate/MedlineDate", xmlValue))
		medlinedate<-lapply(medlinedate_l, function(x) ifelse(class(x)=="list" | class(x)=="NULL", NA, x))
		journal_l<-sapply (a, function(a) xpathSApply(a, "./Article/Journal/Title", xmlValue))
		journal<-lapply(journal_l, function(x) ifelse(class(x)=="list" | class(x)=="NULL", NA, x))
		title_l<-sapply (a, function(a) xpathSApply(a, "./Article/ArticleTitle", xmlValue))
		title<-lapply(title_l, function(x) ifelse(class(x)=="list" | class(x)=="NULL", NA, x))
		author_l<-sapply (a, function(a) xpathSApply(a, "./Article/AuthorList/Author[1]/LastName", xmlValue))
		author<-lapply(author_l, function(x) ifelse(class(x)=="list" | class(x)=="NULL", NA, x))
		return(data.frame(nct_pm=unlist(nct_id), pmid=unlist(pmid), year=unlist(year), month=unlist(month), day=unlist(day),
			year1=unlist(year1), month1=unlist(month1), day1=unlist(day1), medlinedate=unlist(medlinedate), journal=unlist(journal), 
			title=unlist(title), author=unlist(author) ))
	})
}

#-----------------------------------------------------------------------------------------------------------------------------------
# Wrapper function uses batched PMID list and get_pubmed to run pubmed search
# Path takes desired name for folder to save data frames referred to as data files.

fn_pubmed<-function(pmid = pmid_batch, path="pmid_data", from=1, to=max){
	require(plyr)
	max<-length(pmid)
	if (file.exists(path)==FALSE){
		dir.create(path)
	}
	for (i in from:to){
		df<-data.frame()
		df<-get_pubmed(pmid[[i]])
		file<-paste(path, "/data", i,".txt", sep="")
		write.table(df, file=file, sep=";")
	}
}
#-----------------------------------------------------------------------------------------------------------------------------------
fn_pubmed(pmid_batch)
#-----------------------------------------------------------------------------------------------------------------------------------
# Merge back saved tables
fn_merge<-function(path="pmid_data"){
	require(plyr)
	data_files<-list.files(path, full.names=T)
	df<-ldply(data_files, function(x){
		df1<-read.csv(x, header=TRUE, sep=";")
		df2<-data.frame(data_files=gsub(pattern=paste(path, "/", sep=""), replacement="",x), df1)
		return(df2)
	})
	return(df)
}
#-----------------------------------------------------------------------------------------------------------------------------------
# Run
data<-fn_merge()

30/03/201301/04/2013

Leeds paediatric heart surgery: how much variation is acceptable?

It’s all got very messy in Leeds.

A long-term strategy of the government, supported in general by the health profession, is the concentration of high-risk uncommon surgery in fewer centres. This of course means closing departments in some hospitals currently providing those services. Few are in doubt that child heart surgery is high-risk, relatively uncommon and there are probably too many UK centres performing this highly specialised surgery at the moment. Leeds was one of three UK hospitals identified in an NHS review where congenital heart surgery would stop.

On this background and a vigorous local campaign, a case was won in the High Court which ruled the consultation flawed. That was 7th March 2013 and the ruling was published 3 days ago.

The following day, children’s heart surgery was suspended at Leeds after NHS Medical Director, Sir Bruce Keogh, was shown data suggesting that the mortality rate in Leeds was higher than expected.

There have been rumblings in the cardiac surgical community for some time that all was not well in Leeds … As medical director I couldn’t do nothing. I was really disturbed about the timing of this. I couldn’t sit back just because the timing was inconvenient, awkward or would look suspicious, as it does.

– Sir Bruce Keogh, NHS Medical Director

An “agitated cardiologist” later identified as Professor Sir Roger Boyle, director of the National Institute of Clinical Outcomes Research, told Sir Bruce that mortality rates over the last two years were “about twice the national average or more” and rising.

These data are not in the public domain. Sir Bruce and the Trust faced a difficult decision given the implications of the data. This is complicated by the recent court ruling and strength of public feeling, the recent publication of the Francis report into Mid Staffordshire NHS Foundation Trust and the background of cardiac surgery deaths at Bristol Royal Infirmary between 1984 and 1995.

Is mortality in Leeds higher than expected? What is expected? How much variation can be put down to chance? Is this how a potential outlier should be managed?

Dr John Gibbs, chairman of the Central Cardiac Database and the man responsible for the collection and analysis of the data has said the data are “not fit to be looked at by anyone outside the committee”.

It was at a very preliminary stage, and we are at the start of a long process to make sure the data was right and the methodology was correct. We would be irresponsible if we didn’t put in every effort to get the data right. It will cause untold damage for the future of audit results in this country. I think nobody will trust us again. It’s dreadful.

– Dr John Gibbs, chairman of the Central Cardiac Database

Not surprisingly, a senior cardiologist from Leeds, Elspeth Brown, has come out and said the data are just plain wrong and did not include all the relevant operations.

Twice the national average sounds a lot. is it?

Possibly. It’s difficult to know not seeing the data. Natural variation between hospitals in the results of surgery can and does occur by chance. It is possible to see “twice the national average” as a results of natural variation, disturbing as that may sound. It depends on the number of procedures performed annually – small hospitals have more variation – and whether all cardiac procedures are compared together, as opposed to each individual surgical procedure in isolation.

The challenge is in confidently detecting hospitals performing worse than would be expected by chance, as has been alleged in Leeds. Care needs to be taken to ensure that data are accurate and complete. Account is usually made of differences in the patients being treated and the complexity of the surgery performed (often referred to as case-mix).

The graphs below are “funnel plots” that show differences in mortality after congenital heart surgery in US hospitals. These were published in 2012 by Jacobs and colleagues from the University of South Florida College of Medicine. The open source paper is here, but the graphs come from the final paper here which although behind a paywall, the graphs are freely available (note the final version differs from the open source version).

Each graph is for group of child heart operations of increasing complexity and therefore risk. Upper left are the more straightforward procedures, bottom right more complex. The horizontal axis is the annual number of cases and the vertical axis the mortality as a percentage. Each dot on the graph is a hospital performing that particular type of surgery. If a hospital lies outwith the dotted line (95% confidence interval) then there is a possibility that the mortality rate is different from the average. The further above the top line, the greater the chance. These particular funnel plots are not corrected for case-mix, but this has been done else where in the analysis.

It is easy to see that when a hospital does few cases per year, the natural variation in mortality can be high. On the first graph, there is variation from 0 – 3% between different hospitals and this range increases as the surgery gets riskier. There is less variation between hospitals that do more cases. However, in the second graph even the two hospitals doing around 800 procedures per year, there is a greater than two-fold difference in mortality. On the first plot, twice the national average is 1.2%. There are around 11 hospitals above that level in the US for these procedures, the differences for 9 apparently occuring by chance (within the dotted line). Similar conclusions can be drawn from the other graphs of increasingly risky surgery.

Data for cardiac sugery is published and freely available to the public. At the moment, data for children’s heart surgery is not published separately. The data for Leeds General Surgery can be seen here.

To compare children’s heart surgery in Leeds with other centres, we need to the raw data presented in this form and the data corrected for differences in patients. Other issues may be at play, but with the data in the public domain we will be in a better position to make a judgement as to whether an excess in mortality does indeed exist.